在生产中,工程师们经常需要利用气体状态方程来计算压力容器和管道系统在不同温度和压力下的性能,以确保其安全性和效率,通过气体状态方程,可以了解气体在不同条件下的扩散速率和分布规律。
体积等效
由于泄漏而产生的压差取决于测量系统整体(包括被测物WORK和测试器)的内部体积。这也与测量时间密切相关。
在使用空气泄漏测试仪时,我们使用一个称为体积等效(Ve)的系数来表示测量系统整体中压力变化的原因(由于WORK的内部压力或压差传感器引起的体积变化)。
体积等效可以通过以下方程计算得出。
根据空气泄漏测试仪的型号,可以使用自动泄漏校准器(ALC)或泄漏MASTER来直接测量Ve的值。
Ve=Vw+Vt+{Ks(1+Vw/Vm)+Kw}(101.3+P)
Vw=Vm(WORK和MASTER的体积相同)
Ks=0.01mL/kPa或0.005mL/kPa(取决于型号)
Kw=0mL/kPa(WORK体积无变化)
在以上条件下
Ks(1+Vw/Vm)+Kw=2Ks
|当Ks=0.01mL/kPa时
Ve=Vw+Vt+0.02(101.3+P)
|当Ks=0.005mL/kPa时
Ve=Vw+Vt+0.01(101.3+P)
Ve:体积等效(mL)
Vw:WORK和管道的内部体积(mL)
Vt:测试器的内部体积(mL),Vt=9mL
Ks:传感器每压力单位体积变化的比率(mL/kPa)
Kw:WORK每压力单位体积变化的比率
P:测试压力(kPa)
泄漏率
体积等效和泄漏率Q之间的关系表达式
pic_setting01
Q:泄漏率(mL/min)ΔP:压差(Pa)
Ve:体积等效(mL)T:检测时间(s)
示例:当体积等效为800mL,检测时间为3秒时,测得的压差为15Pa。在这些条件下,泄漏率是多少?
<※注释>
由于泄漏产生的压差与体积等效成反比。
[示例]
当体积等效的比例为1到5时,相同泄漏率下的压差将是5到1。
Q:5mL/min
T:2s
ΔP1=85Pa当Ve=200mL
ΔP2=17Pa当Ve=1000mLpic_setting03
<参考>压力和气体的特性
a.绝对压力:以绝对真空为参考点的压力
例如:PaA,kg/cm²A(或kg/cm²abs),Torr(绝对压力=大气压力+表压)
b.表压:以大气压力为参考点的压力
(正压/负压)例如:PaG,kg/cm²G
c.压差:两个压力之间的差异例如:PaD,kg/cm²D
压力单位
1bar=0.1MPa=1.01972kg/cm²,1Pa=1N/m²,1Torr=1mmHg
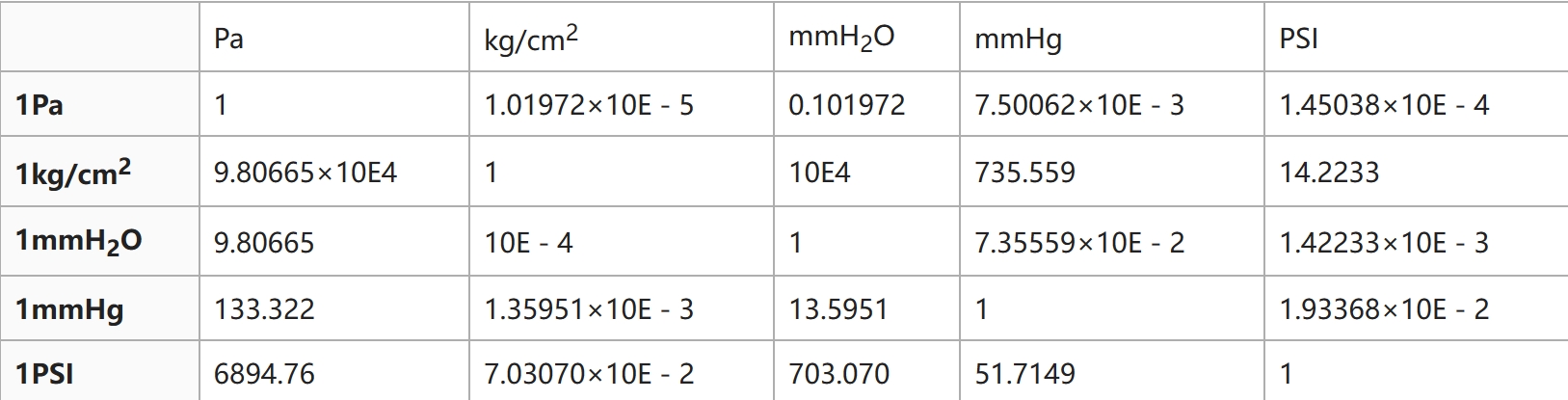
单位转换表:
Pakg/cm²mmH₂OmmHgPSI
1Pa11.01972×10^-50.1019727.50062×10^-31.45038×10^-4
1kg/cm²9.80665×10^4110^4735.55914.2233
1mmH₂O9.8066510^-417.35559×10^-21.42233×10^-3
1mmHg133.3221.35951×10^-313.595111.93368×10^-2
1PSI6894.767.03070×10^-2703.07051.71491
注意:“10E-3”表示10的负三次方
气体的状态方程
气体的压力、体积和温度之间存在恒定的关系。一旦其中两个量确定,另一个量也随之确定。
描述这三个量之间关系的方程被称为状态方程,它基于“气体定律组合”。

PV=GRT…………(1)
在这个方程中:
P:绝对压力
V:体积
G:气体的质量(或摩尔数)
T:绝对温度
R:气体常数
对于初始状态(V1,P1,T1)和最终状态(V2,P2,T2),有以下特殊情况:
如果温度保持不变(T1=T2),则:
P1⋅V1=P2⋅V2………(2)
这被称为波义耳定律(Boyle'sLaw)。
如果体积保持不变(V1=V2),则:
P1/T1=P2/T2………(3)
这被称为查理定律(Charles'Law)。
注意:在实际应用中,我们通常使用理想气体状态方程PV=nRT,其中n是气体的摩尔数,R是通用气体常数(对于所有气体都相同)。但在上述方程中,G被用来表示气体的质量或摩尔数,在大多数工程和科学应用中,使用摩尔数和通用气体常数是更常见的做法。
 Global
Global

